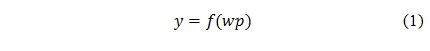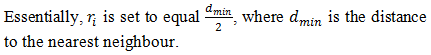For a PDF of this paper click here
Summary
The amount of multi-disciplinary (geology, geophysics, remote sensing, etc.) and multi-parameter geophysical (potential field, EM, gamma-ray spectrometry, etc.) data available for mineral exploration is ever increasing. The integration and analysis of the data require effective and efficient search engines or data mining tools. The search engines will take the signatures of known mineral deposits or interpreted mineralization targets (“key words”), search the data space and return potential new targets (“matches”), thus providing locations to the decision makers for follow-up. Two supervised feed-forward multilayer neural network (NN) search algorithms will be presented and analysed. The utility of the NN search tools will be demonstrated with the integration and analysis of airborne electromagnetic (EM), magnetic and radiometric data for mineralization targets in Iullemmeden Basin, Niger.
Key Words: Search engine, neural network, mineral exploration, Iullemmeden Basin Niger.
Introduction
Integrated airborne geophysical surveys routinely acquire multi-parameter data. Regional and national governments are releasing non-proprietary datasets, including geophysics and geochemistry, and compiling databases of known mineral deposits, (Barnett and Williams, 2012). The amount of multi-disciplinary (geology, geophysics, remote sensing, etc.) and multi-parameter geophysical (potential field, EM, gamma-ray spectrometry, etc.) data available for mineral exploration is ever increasing. The integration and analysis of the data for mineralization targeting require effective and efficient search engines or data mining tools. The ideal search engines will take the signatures of known mineral deposits or interpreted mineralization targets (“key words”), search the data space and return potential new targets (“matches”), thus providing locations to the decision makers for follow-up. In the words of Barnett and Williams (2012), “the most critical decision in exploration is deciding where to look.”
Popular special-purpose search tools that take the magnetic signatures of pipe-like bodies and look for potential kimberlite targets in the magnetic data include the Keating correlation method (Keating, 1995 and Keating and Sailhac, 2004) and three-dimensional Euler deconvolution (Reid et al., 1990, Paterson et al., 1991).
In order to analyse multi-disciplinary or multi-parameter datasets, more general and powerful search engines are required. Supervised neural network (NN) appears to be an ideal search engine for mineral exploration because it possesses the following characteristics discussed in Kasabov (1996):
- NN starts with “no knowledge or memory” and can be trained to search for almost any kind of target;
- NN can take many different inputs, as long as they are numerical;
- NN is robust; if some neurons don’t work due to irrelevant inputs, the whole system may still perform well;
- NN works with partial match; this is perhaps what we really need in exploration as some of the inputs may not possess the target signatures.
NN search engines have been used by Brown et al. (2000), Reford et al. (2004) and Barnett and Williams (2006, 2008) to analyse multi-disciplinary and multi-parameter datasets for mineral targeting.
Two supervised feed-forward multilayer NN search algorithms, recently incorporated into the NN suite described by Reford et al. (2004), will be presented and analysed. The utility of the methods will be demonstrated with the integration and analysis of airborne electromagnetic (EM), magnetic and radiometric data from Niger for mineral exploration targets in Iullemmeden Basin, Niger.
Supervised Feed-Forward Neural Networks
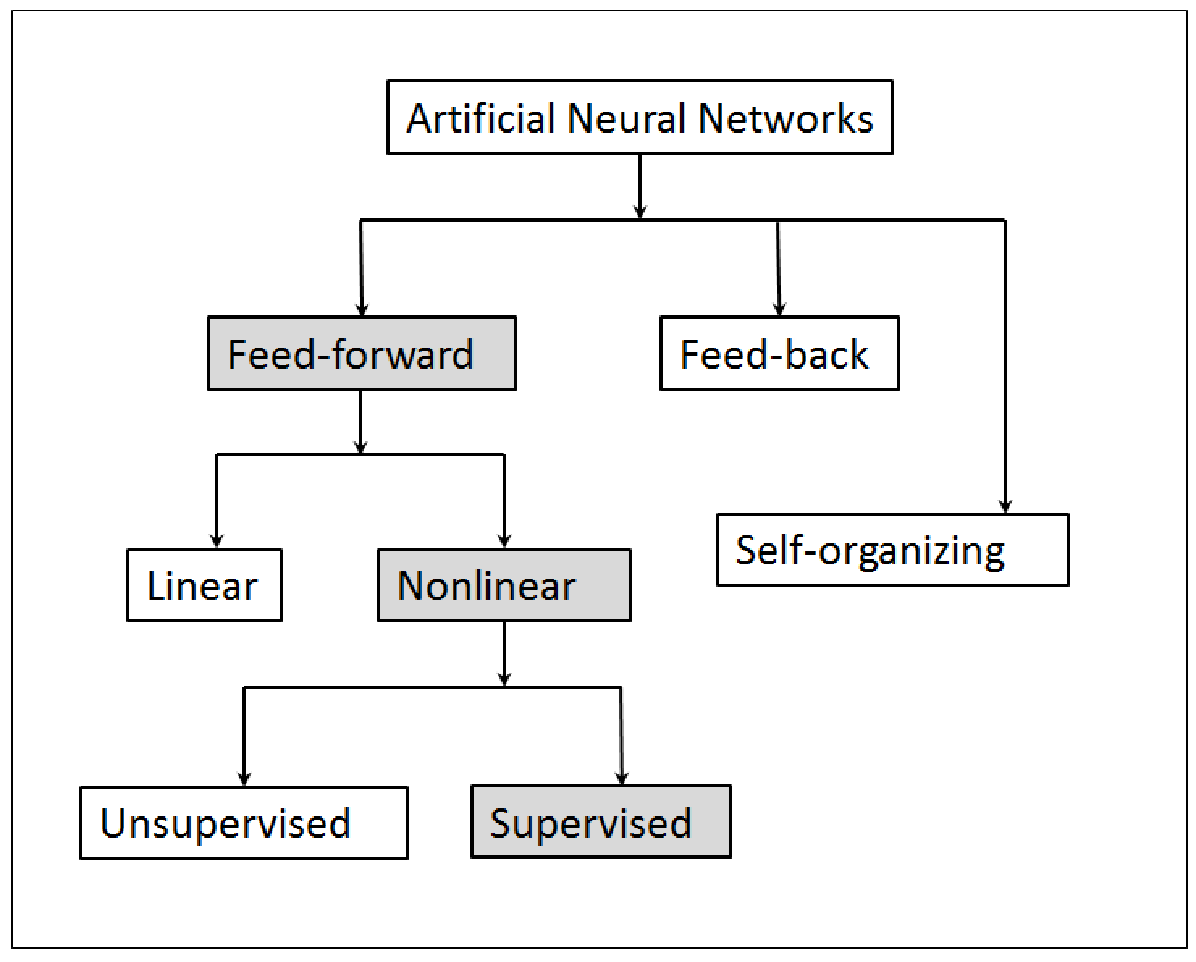
The supervised feed-forward neural networks belong to a sub-class within the domain of artificial neural networks (Figure 1). The word “supervised” means that the training data are specified by the user.
A simple feed-forward neuron, known as a perceptron and first described by Rosenblatt (1958), consists of a scalar input p, a scalar weight w, a scalar output y,
where f is the transfer function. A number of perceptrons can be combined to form a layer of neurons, which can take multiple inputs. A bias can also be added at the summing junction for each perceptron.
Figure 1: Neural networks classifications, modified after Lobbrecht et al., 2002.
A simple feed-forward neural network can consist of just the input and output layers. The most important parameters in a neural network are the weights (Kasabov, 1996). Weights can be obtained by training. There are a number of ways to train a neural network (Haykin, 1999). They include the error-correction and memory-based learning.
Two neural networks are presented and discussed here. The first one is the simple two-layer feed-forward neural network trained by Levenberg-Marquardt (Levenberg, 1944 and Marquardt, 1963) error-correction algorithm (LMNN). The second neural network implemented is the fast classification neural network (FCNN) described by Tang and Kak (2002), which is trained by the memory-based learning method.
Levenberg-Marquardt Error-correction Learning Neural Network (LMNN)
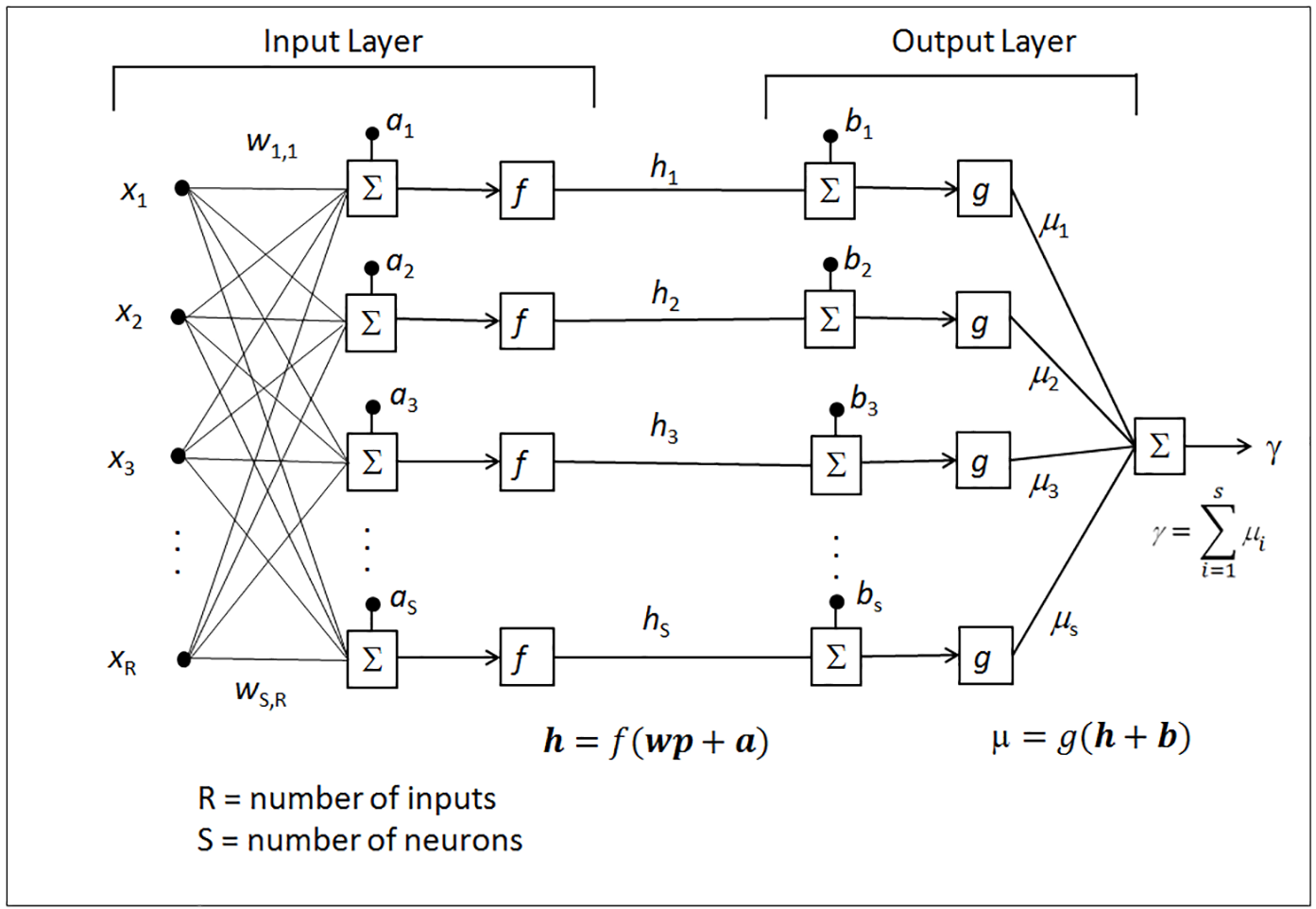
The architecture of a feed-forward two-layer neural network, trained by Levenberg-Marquardt error-correction scheme, is shown in Figure 2. In the input layer, the inputs x, scaled by input weights w, and input biases a are fed into the input transfer function f, producing the first outputs h. The output layer consists of the output transfer function g and the output biases b. The final output g is simply the output of g with the vectors h and b as inputs.
Figure 2: The architecture of Levenberg-Marquardt error-correction learning neural network.
The essence of Levenberg-Marquardt error-correction learning is expressed in equation (2), where the weights vector w is iteratively updated by the error vector e modified by the Jacobian matrix J and the scalar m, which makes the Levenberg-Marquardt method robust.
For LMNN, the input bias vector a are given the values of the error vector e, and the output bias vector b are set to (1-e), thus ensuring the outliers in the inputs are scaled down in importance in the output layer.
It is worth mentioning here that the Levenberg-Marquardt error-correction method is very fast.
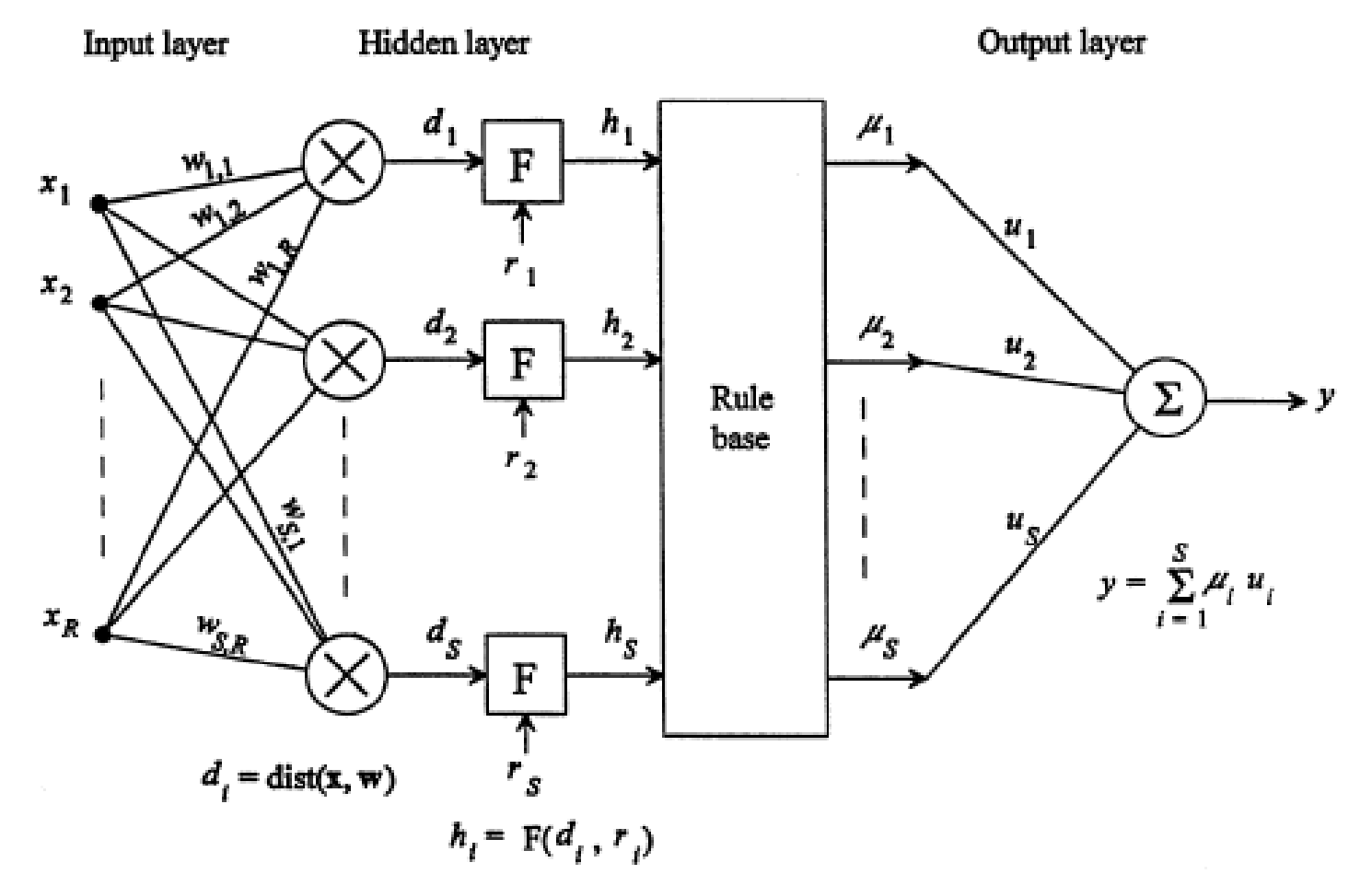
Fast classification Neural Network (FCNN)
The architecture of the fast classification neural network of Tang and Kak (2002) is displayed in Figure 3. The neural network consists of input, hidden and output layers, plus a rule base. There are two sets of weights, input weights and output weights . The hidden layer incorporated the biases , the so-called radius of generalization.
The training of FCNN consists of two steps. During the first step, the input and output weights are prescribed simply by inspection of the training input/output pairs, i.e.,
FCNN simply uses the input and output weights to memorize the training data, thus the so-called memory-based learning. In the second step, the radius of generalization of each hidden neuron is determined, accomplished by another presentation of the training data.
Figure 3: The structure of the fast classification neural network, from Tang and Kak (2002).
The rule base consists of the so-called membership grades, or the degree to which the input x belongs to the output classes, , which is assigned a value using either single-nearest-neighbour or k-nearest-neighbour rule, depending on the number of hidden neuron outputs, , that equal to 0.
LMNN and FCNN Search Results
Test Using Synthetic Data
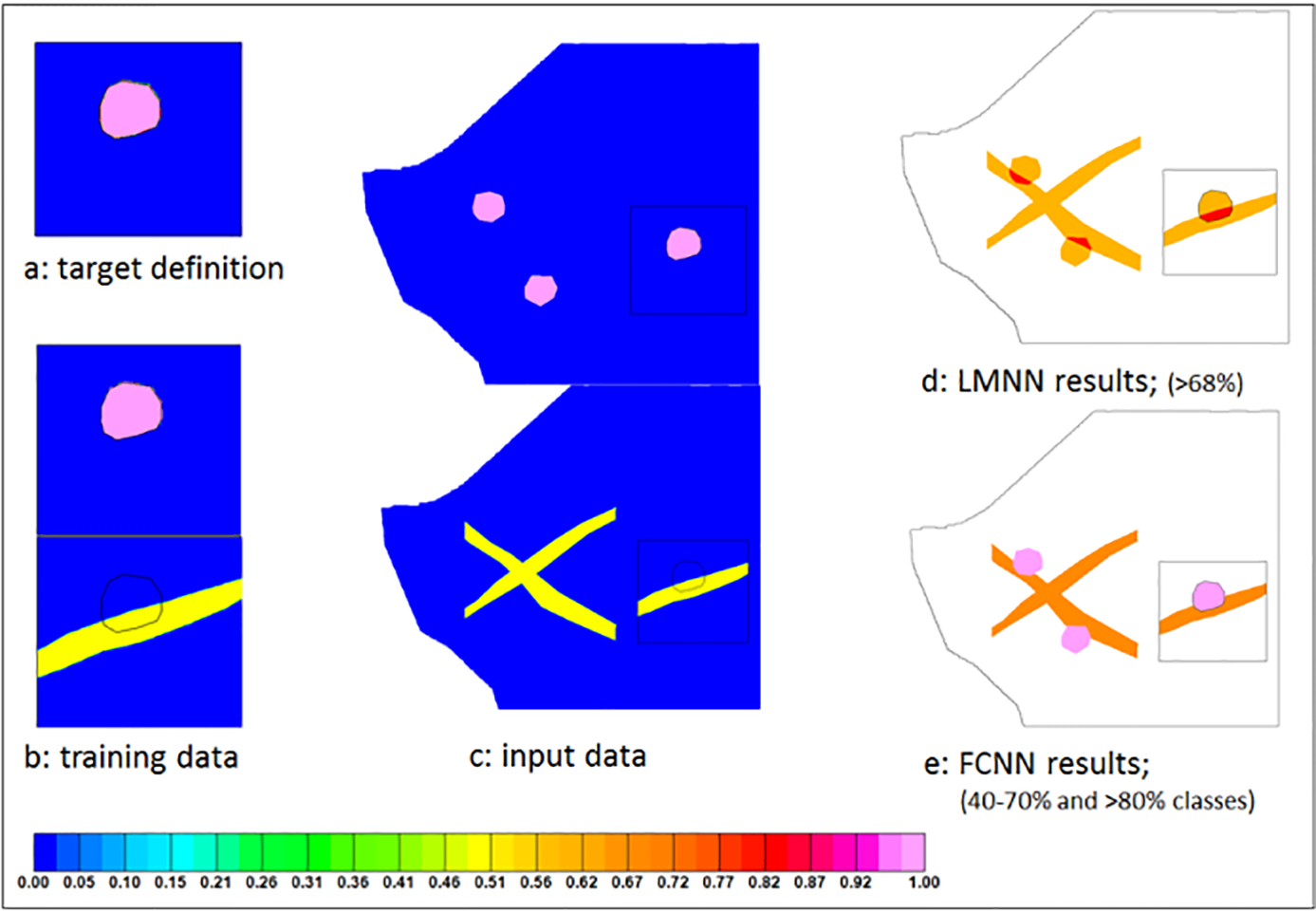
Tests of LMNN and FCNN were conducted using synthetic data, and the search results are shown in Figure 4. The input data must be in grid format. The outputs, the degree of similarity between the grid location and the target, scaled between 0 and 1 (or 100%), are stored in a database. Before running a neural network search, three data processing steps have to be applied.
- Target and training definition grid.
The target and training areas can be defined using polygons. The grid values in the target area are equal to 1, and those outside the target are set to 0. The target can be a known mineralization or an interpreted one, and it should be focused.
- Target and training definition grid
The target and training areas can be defined using polygons. The grid values in the target area are equal to 1, and those outside the target are set to 0. The target can be a known mineralization or an interpreted one, and it should be focused.Training grids - Training Grids
Training grids are the data within the training area. They must all have numerical values. The training grids and the target grid are used to calculate the weights. - Input Grids
Input grids are the actual data to be searched by the trained neural network for potential new targets with signatures similar to those of the target. They must all have numerical values.
Reford et al. (2004) describe the necessity to pre-process the input data and prepare grids that should best discriminate the target of interest rather than simply utilize the measured data grids.
Figure 4: Synthetic data LMNN and FCNN test results.
LMNN and FCNN tests were conducted on two kinds of synthetic data. The first represents localized anomalies, and the second simulates linear features. The goal of the tests is to search for the localized targets, which may represent potential kimberlites. The LMNN search results are shown in (d) of Figure 4, with cut-off at 68%. The results capture all the isolated anomalies, as well as the linear features. The highest search values are located within the overlapping regions of the localized anomalies and the linear features. The FCNN search results are displayed in (e) of Figure 4, which are divided into two classes, one of values between 40% to 80% (orange) and the other of values greater than 80% (hot pink). FCNN is able to identify all the localized targets and separate them from the linear features, because of its classification capability.
Airborne Electromagnetic, Magnetic and Radiometric Data
A fixed-wing airborne magnetic gradiometer and gamma-ray spectrometer survey was flown over Iullemmeden Basin of Niger between June 2012 and July 2013. Detailed helicopter-borne electromagnetic (EM) surveys, flown by Geotech Ltd.’s VTEM time-domain EM system with magnetic gradiometer, were conducted over selected small blocks (Figure 8). The survey project was financed by the European Union, under Project 8 ACP NIR 054, Program to Strengthen and Diversify the Mining Sector in Niger (PRDSM), Europeaid 131447/D/SER/NE.
Geology and Mineralization
The sedimentary series exposed in the Iullemmeden Basin consist mainly of Eocene-Pliocene Continental Terminal and Quaternary formations. The Continental Terminal series, which consist of marine and continental sediments, host considerable amounts of phosphate, lignite and iron ore deposits.
The Precambrian Liptako basement formations outcrop in the western portion of the basin and consist mainly of Birimian volcano-sediments and Proterozoic intrusive formations. The area belongs to the Liptako Metallogenic Province, which hosts several hundreds of mineralized occurrences, including precious and base metals, PGE and REE mineralization (Figure 9).
The West African Craton (WAC) is a well-known kimberlite province. Given the survey area being in or close to the WAC, the potential for locating kimberlitic pipes in Liptako basement is high.
The airborne geophysical data were screened for various types of mineralization potential by the neural networks.
Kimberlite Potential
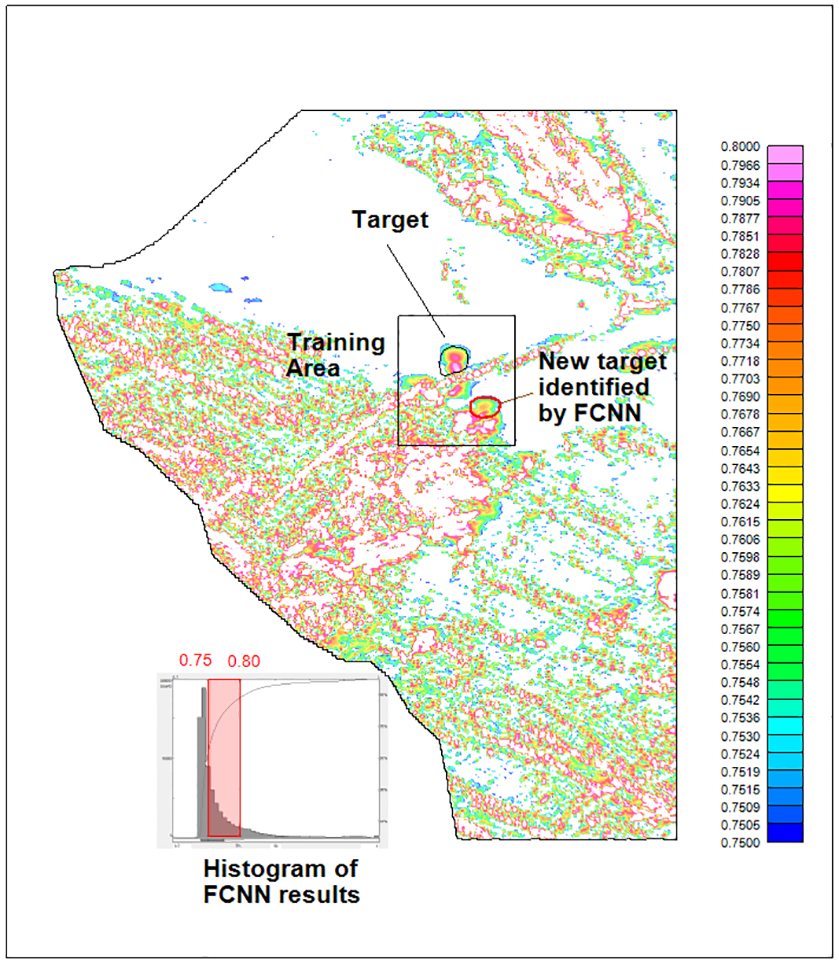
The magnetic data, analytic signal and the first vertical derivative, from the western part of the survey belonging to Liptako basement formations were screened for kimberlite potential by FCNN. The target is a pipe-like body interpreted by the Keating method (Keating and Sailhac, 2004), and the search results are shown in Figure 5. The displayed results belong to a class of NN similarity values between 75% and 80%. FCNN is able to identify a new potential kimberlite target, besides the interpreted one. The linear features in the results are due to the dolerite dykes.
Figure 5: FCNN search results for kimberite potential in Liptako basement.
Iron Ore Analysis
Low grade (30-35% Fe) iron ore resources in Niger are considered as one of the most important in the world. Iron ore occurrences are known to exist in the Iullemmeden Basin. Identifying potential iron ore targets in the airborne magnetic data is one of the most important objectives of the survey project.
The magnetic data, consisting of analytic signal, total horizontal gradient of the tilt-angle, second vertical derivative and total horizontal gradient, are search by LMNN for potential iron ore deposits in the central part of the survey area. The search results help to identify four potential iron ore prospects for follow-up (Figure 6). The target chosen to train the neural network is located in an area with high magnetic gradients. The cut-off of the results for target selection is 54%.
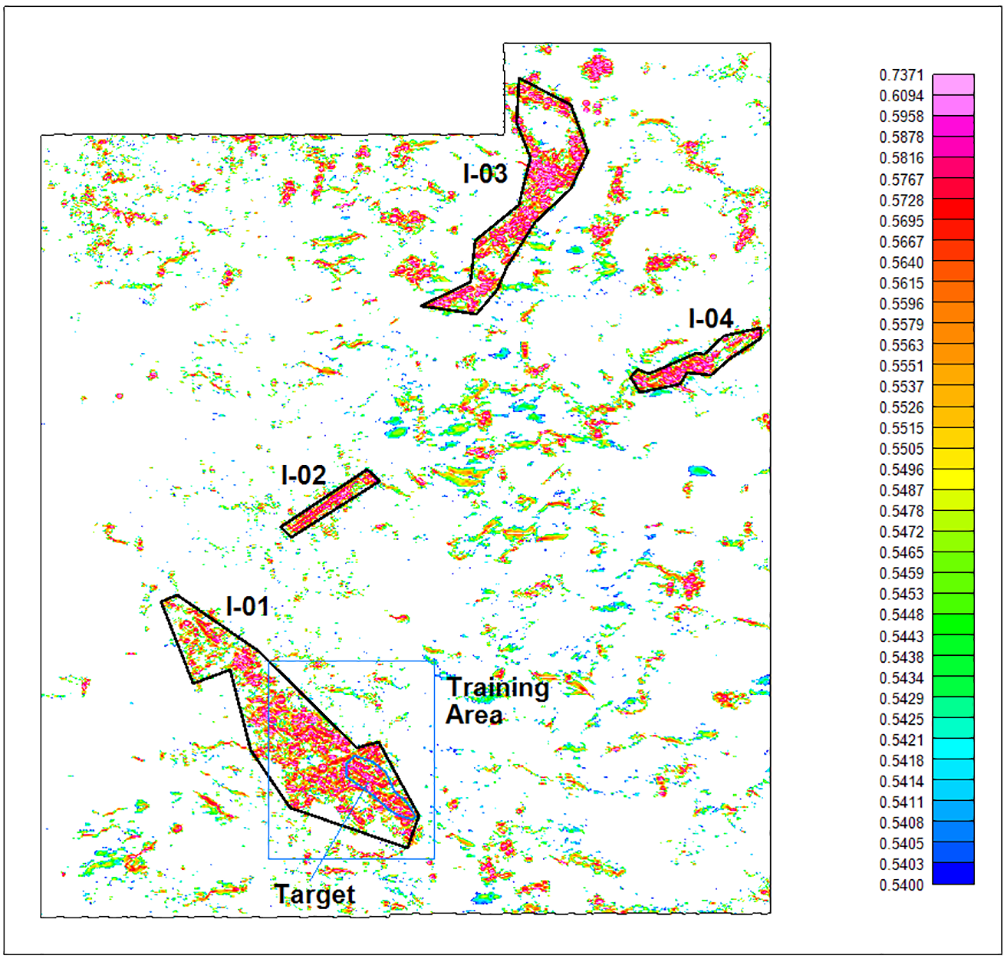
Figure 6: Potential iron ore targets, I-01 to I-04 identified from LMNN search results.Figure 6: Potential iron ore targets, I-01 to I-04 identified from LMNN search results.
Search for Phosphate Targets
Phosphorus (P) is a major element for fertilizer, along with nitrogen (N) and potassium (K). There are many phosphate deposits in sub-Saharan countries, including Niger. In the eastern part of the survey area, phosphate nodules occur in flat-lying Upper Cretaceous to Eocene sediments, deposited in tropical to sub-tropical shallow marine environments. The nodules are encountered with attapulgite as the main clay mineral, which is moderately conductive, and high in hematite content (13%), which is moderately magnetic. Furthermore, phosphrites in general can accommodate a substantial amount of uranium, due to the crystal structure of apatite where uranium substitutes calcium. As a result, phosphates show elevated radioactivity.
For the search of potential phosphate targets, the magnetic (second vertical derivative), electromagnetic (apparent conductivity and time-constant), gamma-ray spectrometric (equivalent uranium concentration), and digital elevation (DEM) data are used. The target area covers two known phosphate occurrences. The LMNN search results for detailed VTEM survey block B2 (Figure 8) are shown in Figure 7, with the cut-off at 90%.
Figure 7: Phosphate search results by LMNN.
Precious and Base Metals Potential in Liptako
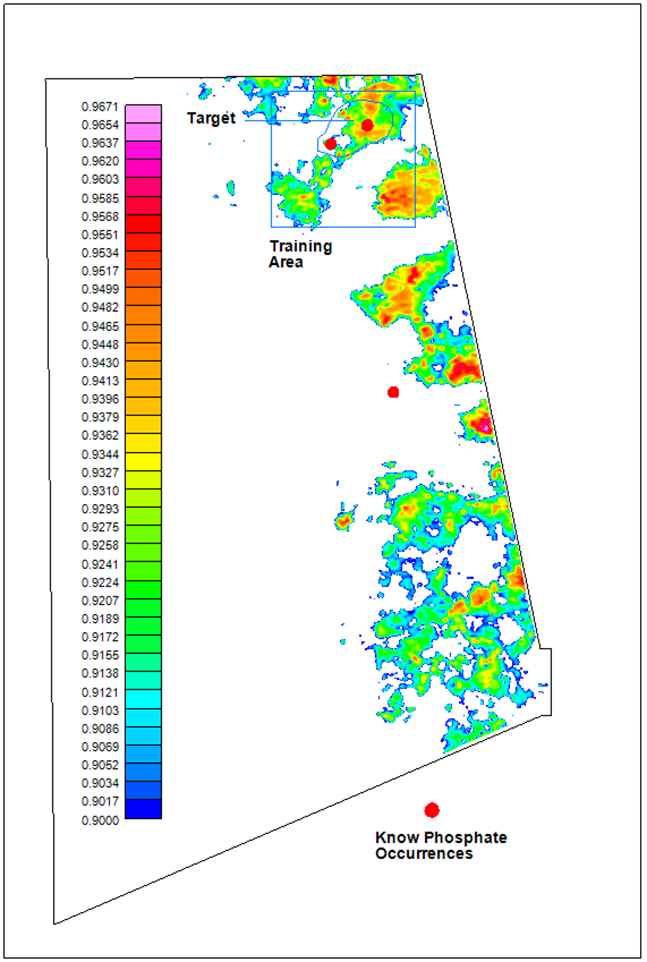
The LMNN method was used to analyse the fixed-wing magnetic and radiometric data, incorporating geology, to assess the precious and base metals potential in the western part of the survey, which belongs to the Liptako Metallogenic Province. The geology is interpretatively transformed into numerical form. Regions with high values are favourable for potential mineralization. The input data include the analytic signal, second vertical derivative, magnetic susceptibility depth slice at 1500m below ground (derived from magnetic 3D inversion), radioelement ratios of percent potassium over equivalent thorium concentration, equivalent uranium concentration over equivalent thorium concentration, and finally the digitized geology. The LMNN search results, with cut-off of 67%, are displayed in Figure 10.
Some of the NN solutions are in close proximity to known mineral occurrences. Others aren’t and those should be followed-up.
This case demonstrates the ability of NN search engines to work with multi-disciplinary data, such as geology. The digitized geology acts as a target selection screen. Similar screens can be devised, using drilling or soil sampling data, for example.
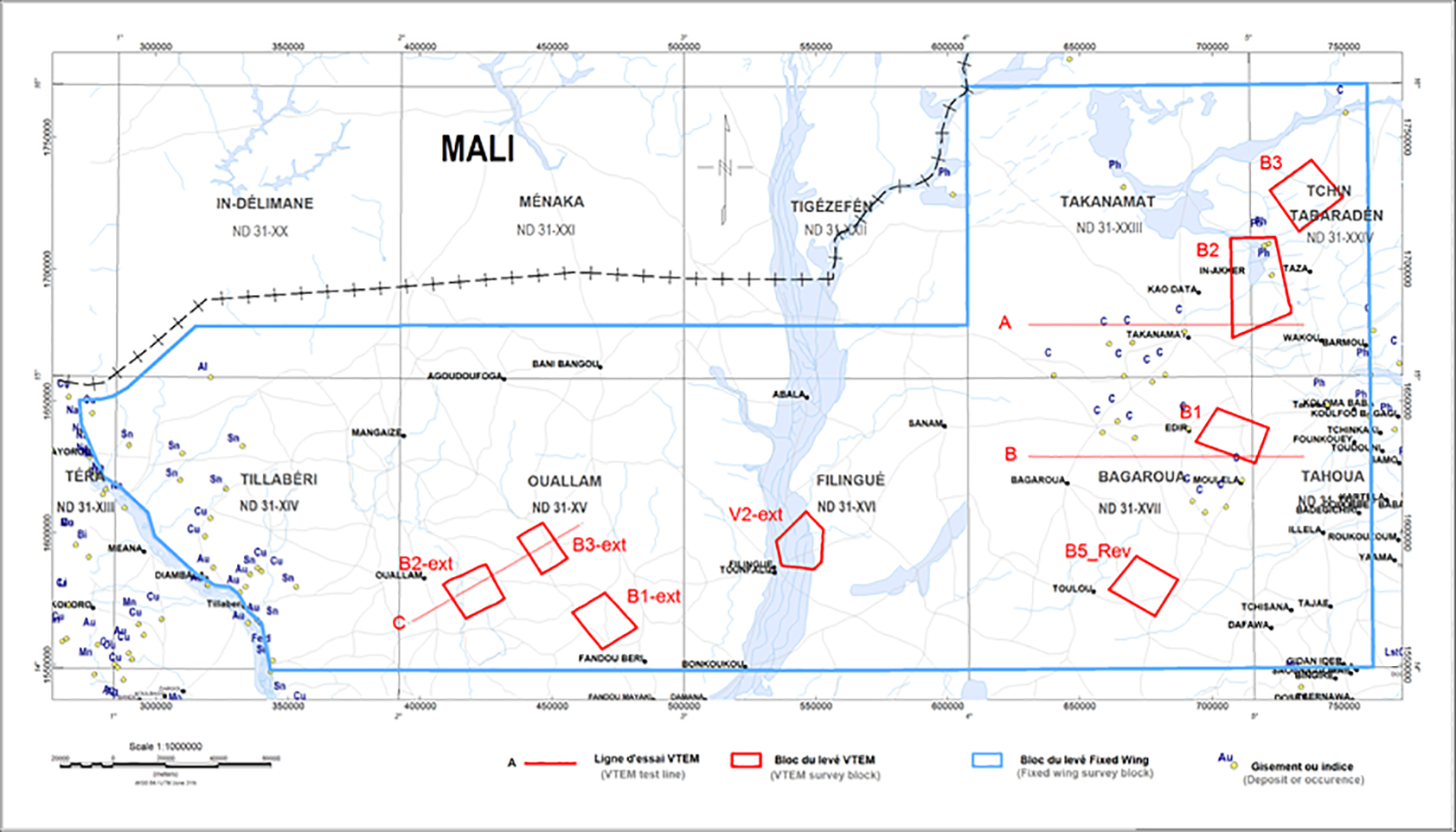
Figure 8: Locations of fixed-wing airborne magnetic and radiometric, and helicopter-borne VTEM surveys in Niger.
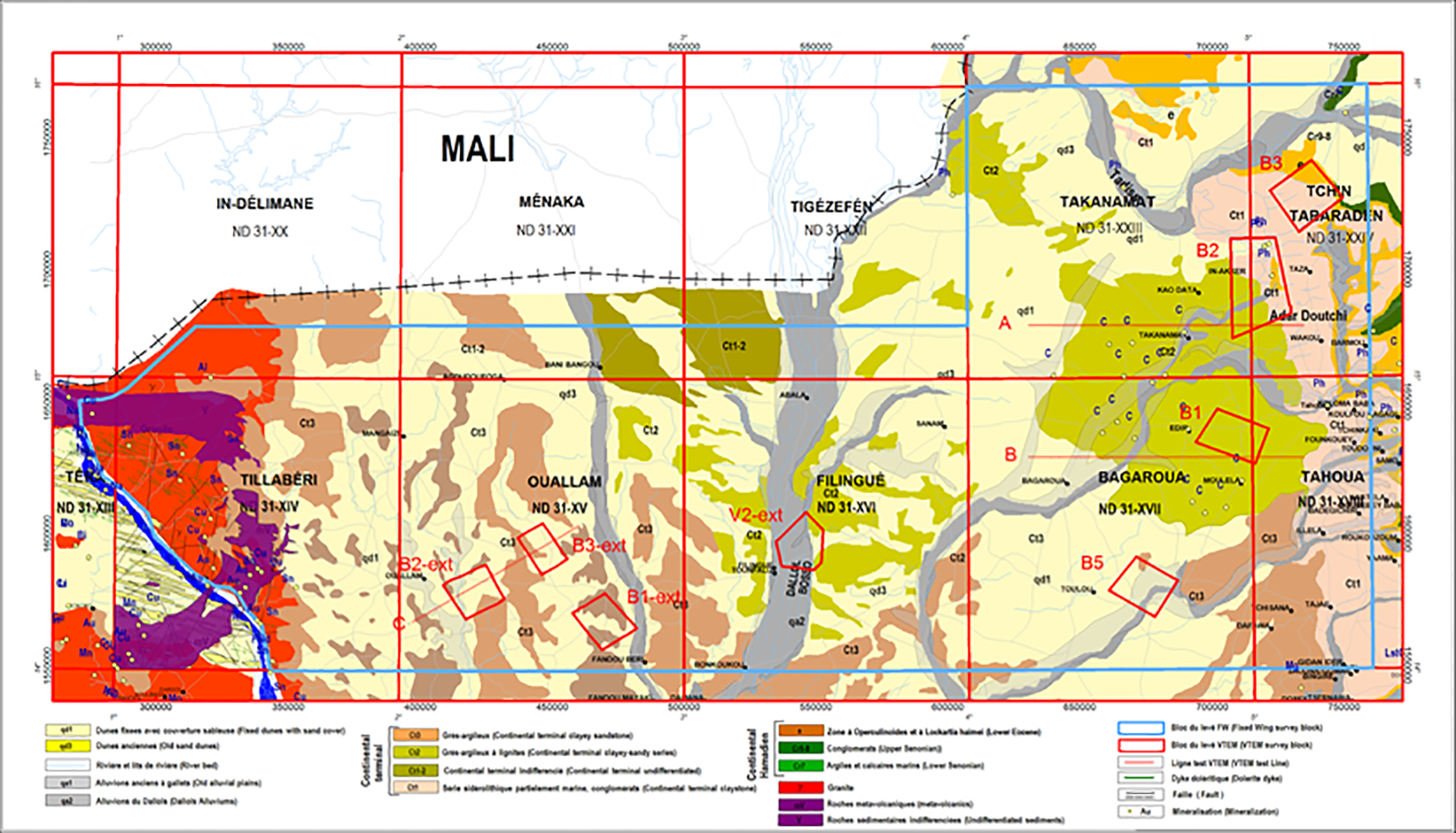
Figure 9: Geology of, after Greigert (1966), and mineralization occurrences in the Iullemmeden Basin.
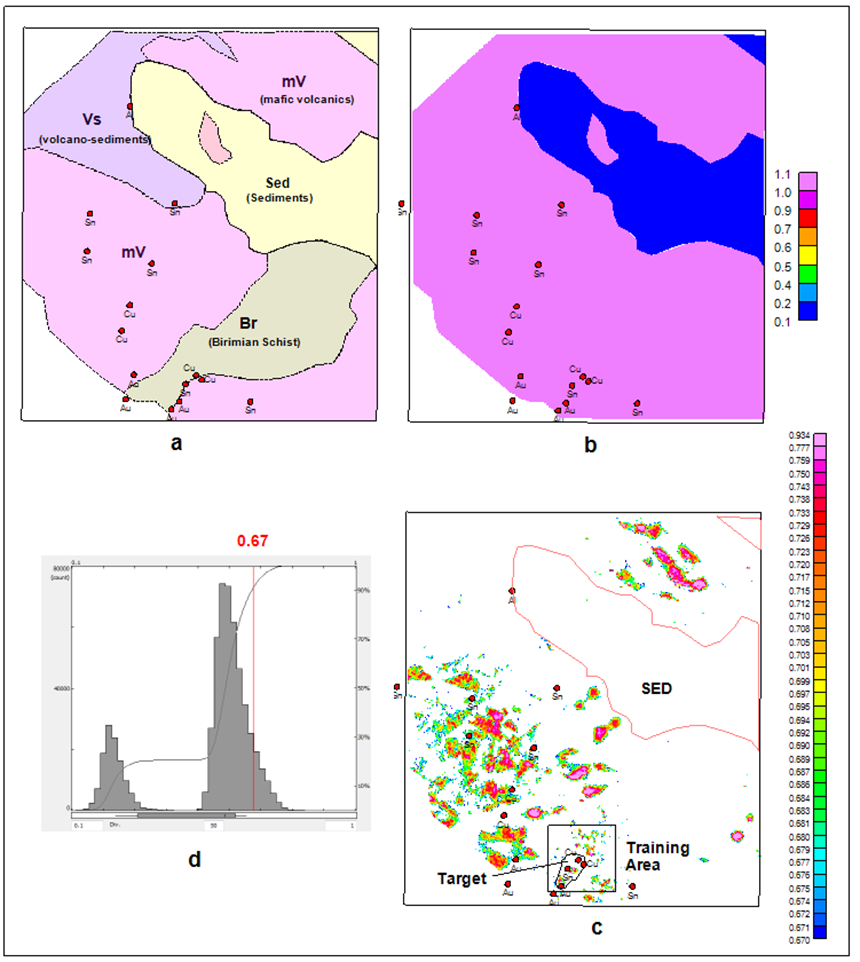
Figure 10: LMNN search results for Liptako Metallogenic Province; a – geology, b – numerically transformed geology from (a), c- LMNN results and the sedimentary areas with very few solutions, and d – histogram of LMNN results and the cut-off point. Most of the solutions with low degree of similarity in are located in the sediments.
Conclusions
Two neural networks, LMNN and FCNN, are presented and analysed using synthetic inputs. The utility of the NNs as search engines for mineral targets is demonstrated with the integrated analysis of airborne geophysical data from Iullemmeden Basin, Niger. The classification capability of the FCNN is particularly suited for the search of kimberlites. Supervised neural networks are powerful search engines for analysing multi-disciplinary and multi-parameter datasets and generating a variety of potential exploration targets for follow-ups. Additional applications of these techniques in Niger showed their effectiveness for mapping geological formations as well.
If exploration target selection can be reduced to a process of elimination, then various selection screens can be setup, using geology, soil sampling, drilling or other data, and be applied either during the NN search or post search. Ultimately, the responsibility of final target selection should always rest with the interpreter.
One of the advantages of NN search engines is their ability to scan through large datasets quickly and in a unified framework. The results from NN search engines are just yet another layer of information for the interpreter to consider.
Acknowledgements
We would like to thank the Ministry of Mines and Industrial Development, Republic of Niger, for permission to use the airborne geophysical survey data from Iullemmeden Basin, Niger, for this study.
References
Barnett, Colin T. and Williams, Peter M., 2012, A radical approach to exploration: Let the data speak for themselves!, Society of Economic Geologists Newsletter, No 90.
Barnett, Colin T. and Williams, Peter M., 2008, The data mining approach to target generation in mature districts, Exploration 2007, www.dmec.ca/ex07-dvd/e07/pdfs/34.pdf, 513-524.
Barnett, Colin T. and Williams, Peter M., 2006, Mineral exploration using modern data mining techniques, Society of Economic Geologists, Special Publication 12, 295-310.
Brown, W.M., Gedeon, T.D., Groves, D.I. and Barnes, R.G., 2000, Artificial neural networks: a new method for mineral prospectivity mapping, Australian Journal of Earth Sciences, 47, 757-770.
Greigert, J., 1966, “Description des Formations Crétacées et Tertiaires du Bassin des Iullemmeden”, Éditions du Bureau de Recherches Géologiques et Minières, Niamey, Publication No.2.
Haykin, Simon, 1999, Neural Networks, A comprehensive foundation, 2nd edition, Pearson Prentice Hall.
Kasabov, Nikola K., 1996, Foundations of Neural Networks, Fuzzy Systems, and Knowledge Engineering, MIT Press, Cambridge, Massachusetts.
Keating, P., and Sailhac, P., 2004, Use of the analytic signal to identify magnetic anomalies due to kimberlite pipes, Geophysics, 69-1, 180-190.
Keating, P., 1995, A simple technique to identify magnetic anomalies due to kimberlite pipes: Exploration and Mining Geology, 4, 121–125.
Levenberg, K., 1944, A method for the solution of certain problems in least squares, Quarterly of Applied Mathematics, 5, 164-168.
Lobbrecht, A.H., et al., (Editors), 2002, Applications of Neural Networks and Fuzzy Logic to integrated water management, project report, IHE, Delft.
Marquardt, D., 1963, An algorithm for least-squares estimation of nonlinear parameters, Society for Industrial and Applied Mathematics Journal on Applied Mathematics, 11-2, 431-441.
Paterson, N. R., Kwan, K. C. H., and Reford, S.W., 1991, Use of Euler deconvolution in recognizing magnetic anomalies of pipe-like bodies: 61st Annual International Meeting Society Exploration Geophysicists, Expanded Abstracts, 642–645.
Reford, S., Lipton, G. and Ugalde H., 2004, Predictive ore deposit targeting using Neural Network analysis, Society of Exploration Geophysicists Expanded Abstracts, 1198-1201.
Reid, A.B., Allsop, J.M., Granser, H., Millet A.J. and Somerton, I.W., 1990, Magnetic interpretation in three dimensions using Euler deconvolution, Geophysics, 55, 80-91.
Rosenblatt, F., 1958, The perceptron: a probabilistic model for information storage and organization in the brain, Psychological Review 65, 386-408.
Tang, K.W. and Kak, S., 2002, Fast classification networks for signal processing, System Signal Processing, 21, 207-224.